Performance Matching
Flap Configurations
As mentioned previously, this design process is an iterative process where designs are constantly reviewed and improved. In this case, the wing were designed after preliminary performance matching and later, flaps were added to perform the performance matching. In the execution of performance matching, the wing airfoil maximum lift coefficient was used. Performance matching was also done with considerations of the various trailing edge and leading edge flap configurations. These configurations would produce different maximum lift which is as follows:
Clean which is represented by CL1 describes conditions where no flaps are deployed.
Deployment of slotted flaps represented by CL2.
Leading-edge flaps are represented with CL3.
Combination of leading-edge flaps and slotted trailing edge flaps represented with CL4.
Plain flaps as represented by CL5.
These maximum lift coefficient values were calculated using the new wing section profile discussed previously. The flap dimensions were already assumed in order to perform this analysis. These measurements can be seen in Figure 1 below.
Figure 1, Flap geometries.
The calculations required for this part utilize Equation 1 seen below where ΔCLmax represents the change in maximum lift coefficient from the original airfoil coefficient.
; (1)
Where ΔClmax can be found in Table 1 (Raymer Table 12.2) shown below[1]. Additionally, ΛHL represents the sweep angle of the flap hinge line.
This equation also requires the areas of wing sections affected by the flaps which are denoted by S_flapped which can be calculated as seen in Figure 2. Similarly, the chord ratio c'/c was also required for more complex flaps which can also be seen in Figure 2.
Figure 2, Geometrical areas needed for the lift change equation [1].
Stall
In this scenario, the altitude of the aircraft is assumed to be close to sea level which validates the assumption that the air's density is equal to the sea level air density.
Various wing flap configurations were taken into account in order to meet 61kt stall speed. The configurations are as follows:
Clean which is represented by CL1 describes conditions where no flaps are deployed.
Deployment of slotted flaps represented by CL2.
Leading-edge flaps are represented with CL3.
Combination of leading-edge flaps and slotted trailing edge flaps represented with CL4.
Initially, the analysis was done with only a clean wing stall in consideration. However, upon reviewing the design's current wing loading, it was determined that most of the performance criteria would not be met without the assistance of flaps. The calculations regarding this parameter can be seen in the Stall Calculations.
As can be seen in the plot, the current design wing loading does not fall within the safe design space without the help of a combination flap. Under clean wing configuration, it is expected that the stall speed would be higher than the expected 61kts.
Stall Calculation
The stall performance matching was done using Equation 2 below.
(2)Assuming clean landing, (CL)MAX can be assumed to be equal to the wing lift coefficient of 1.63. This calculation was performed multiple times with the various different maximum lift coefficients previously found during the flap analysis. The sample below uses the clean wing condition.
Table 2 below shows the different W/S parameters for the various lift coefficients.
| Clean | Slotted | Plain | Leading Edge Flap | Combined | |
| W/S (lb/sq.ft) | 20.515 | 26.409 | 24.595 | 25.549 | 31.444 |
Table 2, Maximum W/S for landing conditions
Takeoff
The take-off distance for the aircraft was determined using historical data of similar aircraft. The plot used for this can be seen in Figure 3 below.
Figure 3, Landing distance of similar aircraft vs maximum take-off weight.
Since the maximum take-off weight has already been determined, the take-off distance can be determined using the best-fit equation from Figure 3 above. This take-off distance assuming 8767lb MTOW was 2059.52 ft. From here, the Takeoff Parameter (TOP) was determined using Raymer's figure 5.4 using the propeller over 50 ft line. This can be seen in Figure 4 of the take-off Calculations section.
As seen in the plot, having a full combination wing configuration allows the aircraft to safely take off with higher power loading. This also allows for the aircraft to take off with the expected take-off distance and have a relatively short ground roll. In this case, an increase in wing loading must be compensated with lower power loading to be able to take off safely with the expected distances.
Takeoff Calculations
Figure 4.1, Takeoff measurement values.
In order to perform the calculation, the TOP must first be calculated. This was done using Raymer's Figure 5.4, seen below.
Figure 4.2, TOP table from Raymer and a scaled ruler to calculate the value [1].
Once the TOP was found, Equation 3 below was used to calculate the maximum wing loading. The TOP for the aircraft was found to be roughly 213 with a takeoff distance of 2000 ft and a ground roll of 1200 ft.
Where σ is the air density ratio between the altitude density and sea level air density. Another coefficient is CLTO, which is the maximum lift coefficient at takeoff, assumed to be 0.92 * CL Landing = 0.92 * CMax. Note that the equation provides P/W, which means the equation must be corrected to reflect a relationship between W/S and W/P. This can be done by plotting the equation: W/S = Coefficient * (W/P)-1.
The summary table can be seen in Table 3 below.
Table 3, Summary of the takeoff performance matching.
Landing
Similarly to the takeoff distance, the landing distance clearing a 50 ft obstacle was also found using data acquired from research on similar aircraft, as seen in Figure 5 below.
Figure 5, Similar aircraft landing distances.
As previously mentioned, the landing distance can be calculated from the best-fit line using the known MTOW value for the aircraft design. This resulted in a landing length of 1585 ft. Assuming an approach distance Sa of 600 ft, which conforms to general aviation values, the ground roll was determined to be 985 ft. The equations regarding this calculation can be seen in the Landing Calculations section. Figure 6 also shows the different landing parameters required for this analysis.
This plot bears a lot of similarity to the stalled plot seen previously. As seen previously, the wing loading for landing falls outside of the safe design space without the assistance of both leading edge and trailing edge flaps. This parameter does not relate to the power loading as it is assumed that the aircraft will land with power off. The landing ground roll can also be reduced in practice using airbrakes and propeller pitch changes.
Landing Calculations
Figure 5.1, Landing parameters.
With reference to Figure 5.1 above, the landing performance matching can be performed using Equation 4 below.
Where σ is the air density ratio between the altitude density and sea level air density. In this equation, WLanding is the landing weight, which is typically a fraction of the MTOW. This value varies depending on the application, but in this scenario, it was assumed to be 97% of the MTOW. The summary of this analysis can be seen in Table 4 below.
Table 4, Landing maximum W/S values for various flap configurations.
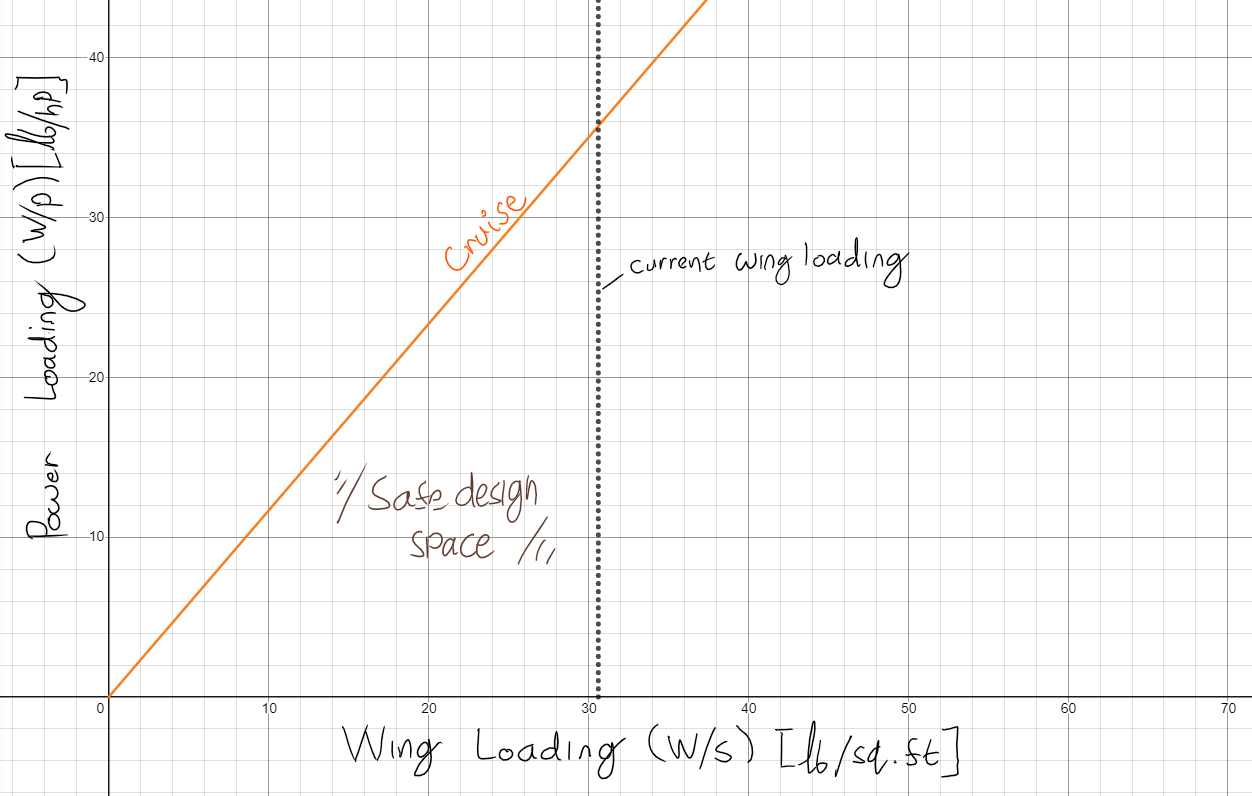
Cruise
Just like in previous methodologies, the cruise performance of the aircraft was determined from historical data. This cruise performance is quantified using the power index IP, which can be found using the figure below, courtesy of Moran, Figure 6.2.
Figure 6, Index parameter plot [2].
Only a single plot is produced with this analysis as the cruise depends only on the wing size, lift, drag, and power of the aircraft. with the current wing loading, there is a large room for freedom for the power loading.
Cruise Calculations
Once the power index was calculated, the cruise performance slope can be plotted using Equation (5).
Here, the wing loading and cruise loading are based on the initial takeoff weight. In this scenario, only one value was acquired as a constant to replace Ip3σ, which was found to be 0.857375.
Additional Conditions
Additionally, power loading for VTOL configuration must also be considered since it was part of the original design requirement. Raymer in his book has described the methods of power sizing for helicopters along with their disk loading (similar idea to wing loading). However, this aircraft is a tilt-rotor which made Raymer's sizing methods to be slightly more difficult to perform. The disk loading of the aircraft was calculated assuming each of the propeller/rotors has a radius of 7.5ft. Raymer however, has also tabulated various typical power loading values as presented in table 21.1. For this aircraft, it was assumed that the wing loading cannot be any higher than 4 lb/hp as it assumes the worst-case scenario. As seen in the plot, it has significantly reduced the design space in order to perform vertical take-off and landing.
Performance Design Envelope
The design envelope requires the aircraft to have considerable low wing loading compared to the researched similar aircraft. This was due to the VTOL requirement which requires the aircraft to have sufficient power to vertically climb. Due to the limitation in engine weight as well as fuel consumption, it would be wise to select the maximum power loading possible in the design envelope. As seen in the composite plot, the current wing loading falls within the safe design space which allowed for the geometry to be kept as is after the second revision. A composite plot for the research aircraft can be seen in Figure 7.
With this in mind, the maximum power loading would be 4lb/hp with a wing loading of 30.62 lb/sq.ft. This meant that the aircraft, with an MTOW of 8767.504lb, would require a total of roughly 2200 hp. Since the aircraft utilizes 2 engines, this would mean that each engine must at least have 1100hp which indicates turbine engines as the only viable option.
Research Aircraft Composite Plot
Figure 7, Composite plot of various aircraft.
References
[1] D. Raymer, Aircraft Design: A Conceptual Approach, Sixth Edition. Washington, DC: American Institute of Aeronautics and Astronautics, Inc., 2018.
[2] L. K. Loftin, “Subsonic Aircraft: Evolution and the Matching of Size To Performance.,” NASA Reference Publication, no. 1060, 1980.